Pembahasan Matematika IPS UN 2016 No. 36 - 40

Pembahasan soal-soal Ujian Nasional (UN) tahun 2016 bidang studi Matematika SMA-IPS nomor 36 sampai dengan nomor 40 tentang:

• simpangan rata-rata, 
• permutasi, 
• kombinasi, 
• frekuensi harapan, dan 
• peluang kejadian.

Soal No. 36 tentang Simpangan Rata-rata

Diketahui data pengukuran terhadap lebar 8 lembar daun cengkeh adalah 4, 5, 6, 3, 7, 5, 8, dan 2 (dalam cm). Simpangan rata-rata dari data tersebut adalah ….

A.   1/4 cm
B.   1/2 cm
C.   3/4 cm
D.   1 cm
E.   3/2 cm

Pembahasan

Rata-rata dari data tersebut adalah:

Simpangan rata-rata dirumuskan sebagai:

Jadi, Simpangan rata-rata dari data tersebut adalah 3/2 cm (E).

Soal No. 37 tentang Permutasi

Dalam lomba catur tingkat sekolah terdapat 10 orang finalis untuk memperebutkan juara I, II, dan III. Banyak susunan juara yang mungkin terjadi adalah ….

A.   720
B.   270
C.   120
D.   60
E.   30

Pembahasan

Karena juara I, II, dan III kedudukannya bertingkat maka soal tersebut harus diselesaikan dengan permutasi, yaitu 10 permutasi 3.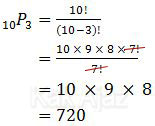

Jadi, banyak susunan juara yang mungkin terjadi adalah 720 (A).

Soal No. 38 tentang Kombinasi

Dari 6 orang siswa akan dipilih 3 orang untuk mengikuti lomba debat. Banyak cara yang mungkin dilakukan adalah ….

A.   8
B.   9
C.   10
D.   15
E.   20

Pembahasan

Tiga orang yang dipilih tersebut tidak ditentukan tingkatannya. Ketiganya mempunyai kedudukan yang setara. Sehingga harus diselesaikan dengan kombinasi, yaitu 6 kombinasi 3.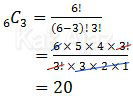

Jadi, banyak cara yang mungkin dilakukan adalah 20 cara (E).

Soal No. 39 tentang Frekuensi Harapan

Tiga keping uang logam setimbang dilempar undi sebanyak 120 kali. Frekuensi harapan kejadian muncul paling sedikit dua angka adalah ….

A.   40
B.   50
C.   60
D.   65
E.   70

Pembahasan

Ruang sampel seluruh kejadian yang mungkin adalah:

S     = AAA, AAG, AGA, GAA, AGG, GAG, GGA, GGG
n(S) = 8

Misal M adalah kejadian muncul paling sedikit dua angka:

M      = AAA, AAG, AGA, GAA
n(M) = 4

Peluang kejadian M adalah:

P(M) = n(M) : n(S)
          = 4/8
          = 1/2

Frekuensi harapan kejadian M adalah:

f_h(M) = P(M) × N
          = 1/2 × 120
          = 60

Jadi, frekuensi harapan kejadian muncul paling sedikit dua angka adalah 60 kali (C).

Soal No. 40 tentang Peluang Kejadian

Dua buah dadu dilempar undi secara bersamaan satu kali. Peluang muncul jumlah mata dadu kurang dari 4 atau lebih dari 9 adalah ….

A.   9/36
B.   12/36
C.   16/36
D.   18/36
E.   24/36

Pembahasan

2 dadu (sisi 6) dilempar bersama:

n(S) = 6²
        = 36

Misal A adalah kejadian muncul jumlah mata dadu kurang dari 4:

A     = (1, 1), (1, 2), (2, 1)
n(A) = 3

Peluang kejadian A adalah:

P(A) = n(A) : n(S)
         = 3/36

Misal B adalah kejadian muncul jumlah mata dadu lebih dari 9:

B     = (4, 6), (5, 5), (5, 6), (6, 4), (6, 5), (6, 6)
n(B) = 6

Peluang kejadian B adalah:

P(B) = n(B) : n(S)
        = 6/36

Peluang kejadian A atau B adalah:

P(A∪B) = P(A) + P(B)
              = 3/36 + 6/36
              = 9/36

Jadi, Peluang muncul jumlah mata dadu kurang dari 4 atau lebih dari 9 adalah 9/36 (A).

Simak Pembahasan Soal Matematika IPS UN 2016 selengkapnya.

No. 01 - 05	No. 21 - 25
No. 06 - 10	No. 26 - 30
No. 11 - 15	No. 31 - 35
No. 16 - 20	No. 36 - 40

Simak juga:
Pembahasan Matematika IPS UN 2014
Pembahasan Matematika IPS UN 2015
Pembahasan Matematika IPS UN 2017
Pembahasan Matematika IPS UN 2018
Pembahasan Matematika IPS UN 2019

Dapatkan pembahasan soal dalam file pdf  di sini.

Demikian, berbagi pengetahuan bersama Kak Ajaz. Silakan bertanya di kolom komentar apabila ada pembahasan yang kurang jelas. Semoga berkah.