Pembahasan Matematika IPS UN 2016 No. 11 - 15

Pembahasan soal-soal Ujian Nasional (UN) tahun 2016 bidang studi Matematika SMA-IPS nomor 11 sampai dengan nomor 15 tentang:

• invers fungsi, 
• sistem pertidaksamaan linear, 
• model matematika program linear, 
• penyelesaian program linear, dan 
• kesamaan matriks.

Soal No. 11 tentang Invers Fungsi

Diketahui

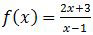
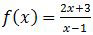
untuk x ≠ 1 dan f⁻¹ adalah invers dari f. Nilai dari f⁻¹(−3) adalah ….

A.   −6
B.   −6/5
C.   0
D.   6/5
E.   6

Pembahasan

Invers fungsi bentuk pecahan linear di atas dapat diselesaikan dengan rumus: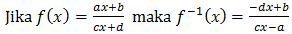

Berdasarkan rumus di atas, diperoleh:

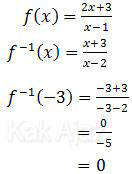
Jadi, nilai dari f⁻¹(−3) adalah 0 (C).

Soal No. 12 tentang Sistem Pertidaksamaan Linear

Nilai minimum dari f(x, y) = 3x + 6y yang memenuhi sistem pertidaksamaan 4x + y ≥ 24; x + y ≥ 9; x ≥ 0; dan y ≥ 0 adalah ….

A.   144
B.   124
C.   39
D.   27
E.   19

Pembahasan

Gambar daerah sistem pertidaksamaan di atas adalah sebagai berikut: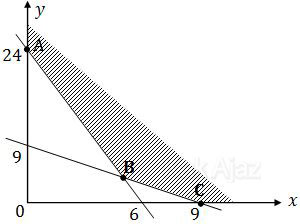

Nilai minimum yang mungkin pada sistem pertidaksamaan di atas berada di titik A, B, atau C.

Sekarang perhatikan fungsi objektifnya!

f(x, y) = 3x + 6y

Koefisien x pada fungsi objektif di atas jauh lebih kecil dari koefisien y. Sehingga dapat dipastikan nilai minimumnya berada di sumbu x, yaitu titik C(9, 0).

f(9, 0) = 3×9 + 6×0
          = 27

Jadi, nilai minimum fungsi objektif pada sistem pertidaksamaan tersebut adalah 27 (D).

Soal No. 13 tentang Model Matematika Program Linear

Setiap hari seorang pasien harus mengonsumsi minimal 400 gram kalsium dan 250 gram vitamin A. Setiap tablet mengandung 150 gram kalsium dan 50 gram vitamin dan setiap kapsul mengandung 200 gram kalsium dan 100 gram vitamin A. Jika dimisalkan banyak tablet x dan kapsul y, model matematikanya adalah ….

A.   3x + 4y ≥ 8;  x + 2y ≥ 5;  x ≥ 0;  y ≥ 0
B.   3x + 4y ≥ 8;  2x + 4y ≥ 5;  x ≥ 0;  y ≥ 0
C.   4x + 3y ≥ 8;  2x + y ≥ 5;  x ≥ 0;  y ≥ 0
D.   4x + 3y ≥ 8;  x + y ≥ 5;  x ≥ 0;  y ≥ 0
E.   4x + 2y ≥ 8;  3x + y ≥ 5;  x ≥ 0;  y ≥ 0

Pembahasan

Untuk mempermudah menentukan model matematikanya, kita buat tabel bantuan sebagai berikut:

	Tablet (x)	Kapsul (y)
Kalsium	150 3	200 4	400 8
Vitamin A	50 1	100 2	250 5

Keterangan: angka yang dicoret tersebut artinya dibagi 50.

Berdasarkan tabel di atas, diperoleh:

3x + 4y ≥ 8
x + 2y ≥ 5

Jadi, model matematika sistem pertidaksamaan tersebut adalah opsi (A).

Soal No. 14 tentang Penyelesaian Program Linear

Pada sebuah supermarket, seorang karyawati menyediakan jasa pembungkusan kado. Untuk membungkus kado jenis A dibutuhkan 2 lembar kertas pembungkus dan 2 meter pita. Sedangkan untuk membungkus kado jenis B dibutuhkan 2 lembar kertas pembungkus dan 1 meter pita. Tersedia kertas pembungkus 50 lembar dan pita 40 meter. Upah untuk membungkus setiap kado jenis A dan untuk membungkus setiap kado jenis B berturut-turut adalah Rp5.000,00 dan Rp4.000,00. Upah maksimum yang dapat diterima oleh karyawati tersebut adalah ….

A.   Rp75.000,00
B.   Rp100.000,00
C.   Rp115.000,00
D.   Rp125.000,00
E.   Rp160.000,00

Pembahasan

Misal:

x : kado jenis A
y : kado jenis B

Tabel bantuan untuk soal di atas adalah:

	Kado A (x)	Kado B (y)
Kertas	2 1	2 1	50 25
Pita	2	1	40
Upah	5.000	4.000	?

Berdasarkan tabel bantuan di atas diperoleh:

  x + y = 25
2x + y = 40
⎯⎯⎯⎯⎯⎯⎯  −  (bawah dikurangi atas)
         x = 15

Substitusi x = 15 ke persamaan yang pertama diperoleh:

  x + y = 25
15 + y = 25
        y = 15

Dengan demikian, upah pembungkusan kado adalah:

Upah = 5.000x + 4.000y
         = 5.000×15 + 4.000×10
         = 75.000 + 40.000
         = 115.000

Jadi, upah maksimum yang dapat diterima oleh karyawati tersebut adalah Rp115.000,00 (C).

Soal No. 15 tentang Kesamaan Matriks

Diketahui matriks:

Jika 2A − B = C^T dengan C^T adalah transpos dari matriks C, nilai x + y = ….

A.   −5
B.   −3
C.   −1
D.   1
E.   5

Pembahasan

Transpos suatu matriks adalah komponen baris matriks tersebut yang diposisikan sebagai komponen kolom.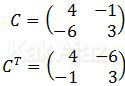

Nah, sekarang kita masuk ke kesamaan matriks.

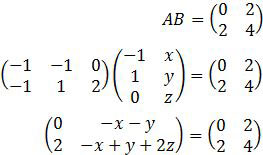
Perhatikan komponen kanan bawah!

2x + 13 = 3
        2x = −10
          x = −5

Sekarang perhatikan kiri bawah!

−3y + 5 = −1
      −3y = −6
          y = 2

Dengan demikian, nilai x + y adalah:

x + y = −5 + 2
         = −3

Jadi, nilai dari x + y adalah −3 (B).

Simak Pembahasan Soal Matematika IPS UN 2016 selengkapnya.

No. 01 - 05	No. 21 - 25
No. 06 - 10	No. 26 - 30
No. 11 - 15	No. 31 - 35
No. 16 - 20	No. 36 - 40

Dapatkan pembahasan soal dalam file pdf  di sini.

Demikian, berbagi pengetahuan bersama Kak Ajaz. Silakan bertanya di kolom komentar apabila ada pembahasan yang kurang jelas. Semoga berkah.