- limit fungsi,
- turunan fungsi,
- fungsi naik atau turun,
- aplikasi turunan, dan
- integral tak tentu.
Soal No. 26 tentang Limit Fungsi
Nilai
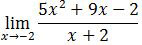
adalah ….
A. −11
B. −1
C. 0
D. 9
E. 11
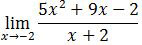
adalah ….
A. −11
B. −1
C. 0
D. 9
E. 11
Pembahasan
Ada dua cara menyelesaikan limit fungsi di atas, yaitu cara pemfaktoran dan penurunan.Cara Pemfaktoran
Pembilang yang berbentuk fungsi kuadrat difaktorkan.
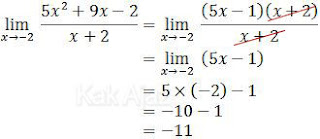
Cara Penurunan
Pembilang dan penyebut masing-masing diturunkan.
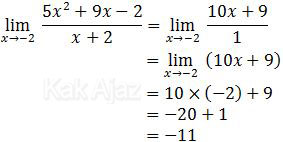
Jadi, nilai dari limit fungsi tersebut adalah −11 (A).
Soal No. 27 tentang Turunan Fungsi
Turunan pertama dari f(x) = (3x2 + 1)3 adalah ….
A. f' (x) = 18x(3x2 + 1)2
B. f' (x) = 18x(3x2 + 1)3
C. f' (x) = 3x(3x2 + 1)2
D. f' (x) = 3x(3x2 + 1)3
E. f' (x) = 6x(3x2 + 1)2
A. f' (x) = 18x(3x2 + 1)2
B. f' (x) = 18x(3x2 + 1)3
C. f' (x) = 3x(3x2 + 1)2
D. f' (x) = 3x(3x2 + 1)3
E. f' (x) = 6x(3x2 + 1)2

Pembahasan
Turunan di atas adalah turunan berantai. Caranya, fungsi yang ada di dalam kurung diturunkan terlebih dahulu. Setelah itu, secara keseluruhan (fungsi pangkat 3) diturunkan.f(x) = (3x2 + 1)3
f' (x) = 6x∙3(3x2 + 1)2
=18x(3x2 + 1)2
Jadi, turunan pertama fungsi f(x) adalah f' (x) = 18x(3x2 + 1)2 (A).
Soal No. 28 tentang Fungsi Naik atau Turun
Fungsi f(x) = ⅔ x3 − x2 − 12x + 12 turun pada interval ….
A. {x│−3 < x < 2, x ∈ R}
B. {x│−2 < x < 3, x ∈ R}
C. {x│x < −3 atau x > 2, x ∈ R}
D. {x│x < −2 atau x > 3, x ∈ R}
E. {x│x < −3 atau x > −2, x ∈ R}
A. {x│−3 < x < 2, x ∈ R}
B. {x│−2 < x < 3, x ∈ R}
C. {x│x < −3 atau x > 2, x ∈ R}
D. {x│x < −2 atau x > 3, x ∈ R}
E. {x│x < −3 atau x > −2, x ∈ R}
Pembahasan
Suatu fungsi akan turun bila turunan fungsi tersebut bernilai negatif.f(x) = ⅔ x3 − x2 − 12x + 12
f' (x) < 0
2x2 − 2x − 12 < 0
x2 − x − 6 < 0
(x − 3)(x + 2) < 0
x = 3 dan x = −2
Karena tanda pertidaksamaannya maka intervalnya berada di antara x = −2 dan x = 3.
−2 < x < 3
Jadi, fungsi f(x) turun pada interval {x│−2 < x < 3, x ∈ R} (B).
Soal No. 29 tentang Aplikasi Turunan
Perusahaan konveksi memproduksi n unit pakaian kemeja dengan biaya total dihitung dengan menggunakan rumus B(n) = 10.000 + 8.000n + 1/3 n2 rupiah. Pakaian kemeja dijual dengan harga Rp60.000,00 per unit. Agar perusahaan tersebut memperoleh keuntungan maksimum, pakaian kemeja harus diproduksi sebanyak ….
A. 12.000 unit
B. 17.000 unit
C. 26.000 unit
D. 78.000 unit
E. 104.000 unit
A. 12.000 unit
B. 17.000 unit
C. 26.000 unit
D. 78.000 unit
E. 104.000 unit
Pembahasan
Biaya total untuk n unit:B(n) = 10.000 + 8.000n + 1/3 n2
Harga jual n unit:
J(n) = 60.000 × n
Keuntungan n unit:
L(n) = J(n) − B(n)
= 60.000n − (10.000 + 8.000n + 1/3 n2 )
= −10.000 + 52.000n − 1/3 n2
Keuntungan maksimum untuk n unit:
L'(n) = 0
52.000 − 2/3 n = 0
2/3 n = 52.000
n = 3/2 × 52.000
= 78.000
Jadi, keuntungan maksimum akan tercapai jika pakaian kemeja diproduksi sebanyak 78.000 unit (D).
Soal No. 30 tentang Integral Tak Tentu
∫(3x2 − 7x − 6) dx = ….
A. x3 − 1/2 x2 − 6x + C
B. x3 + 7x2 + 6x + C
C. x3 + 1/2 x2 + 6x + C
D. x3 − 7/2 x2 − 6x + C
E. x3 − 7/2 x2 + 6x + C
A. x3 − 1/2 x2 − 6x + C
B. x3 + 7x2 + 6x + C
C. x3 + 1/2 x2 + 6x + C
D. x3 − 7/2 x2 − 6x + C
E. x3 − 7/2 x2 + 6x + C
Pembahasan
Dikatakan integral tak tentu karena hasil integralnya masih mengandung konstanta integrasi C.∫(3x2 − 7x − 6) dx
= 3∙1/3 x3 − 7∙1/2 x2 − 6x + C
= x3 − 7/2 x2 − 6x + C
Jadi, hasil integral fungsi tersebut adalah x3 − 7/2 x2 − 6x + C (D).
Simak Pembahasan Soal Matematika IPS UN 2016 selengkapnya.
| No. 01 - 05 | No. 21 - 25 |
| No. 06 - 10 | No. 26 - 30 |
| No. 11 - 15 | No. 31 - 35 |
| No. 16 - 20 | No. 36 - 40 |
Dapatkan pembahasan soal dalam file pdf di sini.
Demikian, berbagi pengetahuan bersama Kak Ajaz. Silakan bertanya di kolom komentar apabila ada pembahasan yang kurang jelas. Semoga berkah.

No comments:
Post a Comment
Maaf, komentar yang tidak berhubungan dengan konten, banyak mengandung singkatan kata, atau mengandung link aktif, tidak kami tayangkan.
Komentar Anda akan kami moderasi sebelum kami tayangkan. Centang 'Notify me' agar Anda mendapat pemberitahuan lewat email bahwa komentar Anda sudah ditayangkan