Pembahasan Matematika IPS UN 2019 No. 16 - 20

Pembahasan soal Ujian Nasional (UN) tahun 2019 bidang studi Matematika SMA-IPS nomor 16 sampai dengan nomor 20 tentang:

• deret geometri tak hingga, 
• suku ke-n deret geometri, 
• bunga majemuk, 
• limit fungsi aljabar, dan 
• limit di titik tak hingga.

Soal No. 16 tentang Deret Geometri Tak Hingga

Jumlah tak hingga dari deret 4 + 3 +  9/4 + 27/16 + 81/64 + ⋯ adalah ….

A.   13/3
B.   16/3
C.   13
D.   16
E.   65/4

Pembahasan

Berdasarkan deret geometri tersebut diperoleh:

a = 4
r = 3/4

Jumlah tak hingga deret geometri dirumuskan:

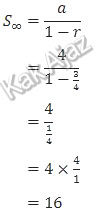
Jadi, jumlah tak hingga dari deret geometri tersebut adalah 16 (D).

Soal No. 17 tentang Suku ke-n Deret Geometri

Diketahui suku ke-3 dan suku ke-6 barisan geometri berturut-turut adalah 12 dan 96. Rumus suku ke-n barisan tersebut adalah ….

A.   U_n = 6 ∙ 2ⁿ⁺¹
B.   U_n = 6 ∙ 2ⁿ
C.   U_n = 3 ∙ 2ⁿ
D.   U_n = 3 ∙ 2ⁿ⁻¹
E.   U_n = 2ⁿ⁻¹

Pembahasan

Diketahui:

U₃ = 12
U₆ = 96

Rasio deret tersebut dapat ditentukan dengan:

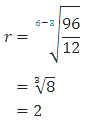
Suku ke-n deret geometri dirumuskan sebagai:

U_n = a ∙ rⁿ⁻¹

Berdasarkan rumus tersebut maka:

     U₃ = 12
  a ∙ r² = 12
a × 2² = 12
      4a = 12
        a = 3

Dengan demikian,

U_n = a ∙ rⁿ⁻¹
      = 3 ∙ 2ⁿ⁻¹

Jadi, rumus suku ke-n barisan tersebut adalah opsi (D).

Soal No. 18 tentang Bunga Majemuk

Modal sebesar Rp2.000.000,00 disimpan di bank dengan suku bunga majemuk 2% per tahun. Besar modal pada akhir tahun kedua adalah ….

A.   Rp2.040.000,00
B.   Rp2.040.400,00
C.   Rp2.080.000,00
D.   Rp2.080.800,00
E.   Rp2.122.400,00

Pembahasan

Diketahui:

M₀ = 2.000.000
    i = 2% = 0,02
   n = 2

Modal pada periode ke-n dirumuskan sebagai:

M_n = M₀ (1 + i)ⁿ
      = 2.000.000 × (1 + 0,02)²
      = 2.000.000 × (1,02)²
      = 2.000.000 × 1,0404
      = 2.080.800

Jadi, besar modal pada akhir tahun kedua adalah Rp2.080.800,00 (D).

Soal No. 19 tentang Limit Fungsi Aljabar

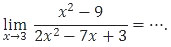
A.   1/2
B.   5/6
C.   6/7
D.   7/6
E.   6/5

Pembahasan

Cara 1 (penjabaran)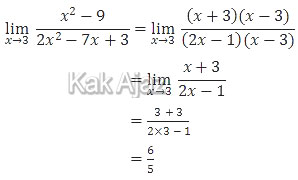

Cara 2 (dalil L’Hopital)
Penyebut dan pembilang masing-masing diturunkan.

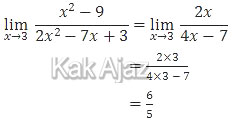
Jadi, limit fungsi aljabar tersebut adalah 6/5 (E).

Soal No. 20 tentang Limit di Titik Tak Hingga

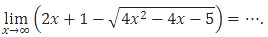
A.   −2
B.   −1
C.   0
D.   1
E.   2

Pembahasan

Bentuk baku dari limit fungsi di atas adalah: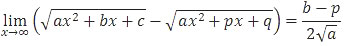

Nah, sekarang kita ubah bentuk limit di atas ke bentuk bakunya.

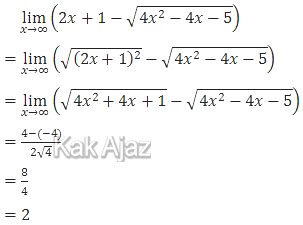
Jadi, nilai limit fungsi tersebut adalah 2 (E).

Simak Pembahasan Soal Matematika IPS UN 2019 selengkapnya.

No. 01 - 05	No. 21 - 25
No. 06 - 10	No. 26 - 30
No. 11 - 15	No. 31 - 36
No. 16 - 20	No. 37 - 40

Dapatkan pembahasan soal dalam file pdf  di sini.

Demikian, berbagi pengetahuan bersama Kak Ajaz. Silakan bertanya di kolom komentar apabila ada pembahasan yang kurang jelas. Semoga berkah.