Pembahasan Matematika IPS UN 2019 No. 21 - 25

Pembahasan soal Ujian Nasional (UN) tahun 2019 bidang studi Matematika SMA-IPS nomor 21 sampai dengan nomor 25 tentang:

• turunan fungsi, 
• aplikasi turunan, 
• integral, 
• segitiga trigonometri, dan 
• kuadran trigonometri.

Soal No. 21 tentang Turunan Fungsi

Turunan pertama fungsi f(x) = (4x² − 12x)(x + 2) adalah ….

A.   f'(x) = 12x² − 4x − 24
B.   f'(x) = 12x² − 8x + 24
C.   f'(x) = 24x − 8
D.   f'(x) = 12x² − 16x + 24
E.   f'(x) = 12x² − 8x − 24

Pembahasan

Sebelum diturunkan, dikalikan dulu saja supaya tidak menurunkan dalam bentuk u∙v.

f(x) = (4x² − 12x)(x + 2)
       = (4x² − 12x)x + (4x² − 12x)2
       = 4x³ − 12x² + 8x² − 24x
       = 4x³ − 4x² − 24x
f'(x) = 4∙3x² − 4∙2x¹ − 24∙1x⁰
       = 12x² − 8x − 24

Jadi, turunan pertama fungsi tersebut adalah opsi (E).

Soal No. 22 tentang Aplikasi Turunan

Grafik fungsi f(x) = x³ + 3/2 x² − 18x + 5 naik pada interval ….

A.   −2< x <3
B.   −3 < x < 2
C.   x < 2 atau x > 3
D.   x < −3 atau x > 2
E.   x < −2 atau x > 3

Pembahasan

Agar suatu fungsi naik maka turunan fungsi tersebut harus lebih dari nol.

f(x) = x³ + 3/2 x² − 18x + 5

               f'(x) > 0
3x² + 3x − 18 > 0
      x² + x − 6 > 0
(x + 3)(x − 2) > 0

Pembuat nol: x = −3 dan x = 2

Karena tanda pertidaksamaannya “>” maka intervalnya berada di sebelah kiri −3 dan di sebelah kanan 2.

x < −3 atau x > 2

Jadi, grafik fungsi tersebut naik pada interval x < −3 atau x > 2 (D).

Soal No. 23 tentang Integral

Hasil dari ∫ (2x³ − 9x² + 4x − 5) dx = ⋯.

A.   ½ x⁴ − 6x³ + 2x² − 5x + C
B.   ½ x⁴ − 6x³ + x² − 5x + C
C.   ½ x⁴ − 3x³ + x² − 5x + C
D.   ½ x⁴ − 3x³ + 2x² − 5x + C
E.   ½ x⁴ − 6x³ − 2x² − 5x + C

Pembahasan

Soal ini Cuma butuh kecermatan dan ketelitian. Mari kita kerjakan secara hati-hati.

∫ (2x³ − 9x² + 4x − 5) dx
= 2 ∙ ¼ x⁴ − 9 ∙ ⅓ x³ + 4 ∙ ½ x² − 5x + C
= ½ x⁴ − 3x³ + 2x² − 5x + C

Jadi, hasil dari integral tersebut adalah opsi (D).

Soal No. 24 tentang Segitiga Trigonometri

Diketahui segitiga ABC siku-siku di A dan sin ⁡B = 3/7. Nilai tan⁡ C adalah ….

A.   3/20 √10
B.   7/20 √10
C.   2/3 √10
D.   3/2 √10
E.   7/3 √10

Pembahasan

Perhatikan gambar di bawah ini!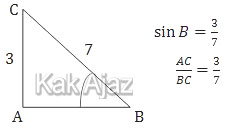

Panjang AB dapat dicari melalui rumus Pythagoras sebagai berikut:

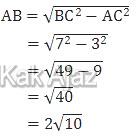
Nilai tan ⁡C merupakan perbandingan antara AB terhadap AC.

Jadi, nilai tan ⁡C adalah 2/3 √10 (C).

Soal No. 25 tentang Kuadran Trigonometri

Nilai dari cos⁡ 300° +sin⁡ 150° − tan⁡ 135° adalah ….

A.   √3 − 1
B.   √3 + 1
C.   0
D.   1
E.   2

Pembahasan

Untuk menyelesaikan soal ini, harus mengingat kembali nilai trigonometri di berbagai kuadran.

Jadi, nilai dari cos⁡ 300° +sin⁡ 150° − tan⁡ 135° adalah 2 (E).

Simak Pembahasan Soal Matematika IPS UN 2019 selengkapnya.

No. 01 - 05	No. 21 - 25
No. 06 - 10	No. 26 - 30
No. 11 - 15	No. 31 - 36
No. 16 - 20	No. 37 - 40

Dapatkan pembahasan soal dalam file pdf  di sini.

Demikian, berbagi pengetahuan bersama Kak Ajaz. Silakan bertanya di kolom komentar apabila ada pembahasan yang kurang jelas. Semoga berkah.