Pembahasan Matematika SMP UN 2018 No. 11 - 15

Pembahasan soal Matematika SMP Ujian Nasional (UN) tahun 2018 nomor 11 sampai dengan nomor 15 tentang:

• aritmetika sosial [bunga bank], 
• perbandingan senilai, 
• perbandingan tiga variabel, 
• skala, dan 
• penjumlahan suku sejenis.

Soal No. 11 tentang Aritmetika Sosial [bunga bank]

Diana menabung uang di bank sebesar Rp8.000.000,00. Setelah 8 bulan uangnya diambil seluruhnya sebesar Rp8.800.000,00. Berapakah persentase suku bunga tabungan yang diberikan bank tersebut?

A.   10%.
B.   12%.
C.   15%.
D.   18%.

Pembahasan

Bunga (b) adalah selisih antara modal akhir dengan modal awal.

b = 8.800.000 − 8.000.000
   = 800.000

Persentase bunga adalah perbandingan bunga terhadap modal awal dalam persen.

Bunga tersebut adalah bunga selama 8 bulan. Pembuat soal tidak menyebutkan bunga per bulan atau per tahun. Kita cari kedua-duanya saja.

Bunga per bulan = 10% : 8
                            = 1.25%

Bunga per tahun = 12/8 × 10%
                            = 15%

Jadi dengan anggapan bunga per tahun, persentase suku bunga tabungan yang diberikan bank tersebut adalah 15% (C).

Soal No. 12 tentang Perbandingan Senilai

Tini memiliki pita sepanjang 1,5 m dan Neni memiliki pita 4.500 cm. Perbandingan pita Tini dan Neni adalah ….

A.   1 : 45
B.   1 : 30
C.   1 : 3
D.   1 : 2

Pembahasan

Untuk membandingkan, satuan harus kita samakan terlebih dahulu.

Jadi, perbandingan pita Tini dan Neni adalah 1 : 30 (B).

Perdalam materi ini di Perbandingan Senilai dan Berbalik Nilai [Soal UN dan Pembahasan].

Soal No. 13 tentang Perbandingan Tiga Variabel

Perbandingan uang Verrel, Saffa, dan Mahesa adalah 4 : 3 : 2. Jika jumlah uang Verrel dan uang Saffa Rp42.000,00 maka jumlah uang mereka bertiga adalah ….

A.   Rp54.000,00
B.   Rp58.000,00
C.   Rp60.000,00
D.   Rp62.000,00

Pembahasan

Cara 1

Anggap saja perbandingan sebenarnya uang mereka adalah:

4x ∶ 3x ∶ 2x

Jumlah uang Verrel dan uang Saffa Rp42.000,00.

4x + 3x = 42.000
        7x = 42.000
          x = 6.000

Dengan demikian jumlah uang Verrel, Saffa, dan Mahesa adalah:

4x + 3x + 2x = 9x
                     = 9 × 6.000
                     = 54.000

Cara 2

Kita bandingkan jumlah uang mereka bertiga terhadap jumlah uang yang diketahui (Verrel dan Saffa).

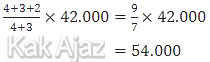
Jadi, jumlah uang mereka bertiga adalah Rp54.000,00 (A).

Perdalam materi ini di Perbandingan Bertingkat [Soal UN dan Pembahasan].

Soal No. 14 tentang Skala

Sebuah peta mempunyai skala 1 : 2.500.000. pada peta tersebut jarak:

• kota A ke kota P = 3 cm,
• kota P ke kota B = 6 cm,
• kota A ke kota Q = 3 cm,
• kota Q ke kota B = 4 cm.

Adi berkendaraan dari kota A ke kota B melalui kota P dan Ali berkendaraan dari kota A ke kota B melalui kota Q.

Berapakah selisih jarak tempuh yang lalui Ali dan Adi?

A.   75 km.
B.   50 km.
C.   25 km.
D.   5 km.

Pembahasan

Jarak yang ditempuh Adi dari kota A ke kota B melalui kota P pada peta adalah:

s₁ = (AP + PB) cm
    = (3 + 6) cm
    = 9 cm

Sedangkan jarak yang ditempuh Ali dari kota A ke kota B melalui kota Q pada peta adalah:

s₂ = (AQ + QB) cm
    = (3 + 4) cm
    = 7 cm

Selisih jarak tempuh keduanya pada peta adalah:

∆s = s₁ − s₂
     = (9 − 7) cm
     = 2 cm

Sedangkan selisih keduanya pada jarak sebenarnya adalah:

∆s = 2 × 2.500.000 cm
     = 5.000.000 cm
     = 50 km

Jadi, selisih jarak tempuh yang dilalui Ali dan Adi adalah 50 km (B).

Perdalam materi ini di Skala [Soal UN dan Pembahasan].

Soal No. 15 tentang Penjumlahan Suku Sejenis

Bentuk sederhana dari 5ab + 4bc − 3ac − 2ac − 8bc − ab adalah ….

A.   4ab - 4bc − 5ac
B.   4ab + 2bc − 11ac
C.   6ab + 2bc − 5ac
D.   6ab − 4bc + 5ac

Pembahasan

Sebelum kita operasikan, kita kelompokkan suku-suku yang sejenis terlebih dahulu.

   5ab + 4bc − 3ac − 2ac − 8bc − ab
= (5ab − ab) + (4bc − 8bc) + (−3ac − 2ac)
= (5 − 1)ab + (4 − 8)bc + (−3 − 2)ac
= 4ab − 4bc − 5ac


Jadi, bentuk sederhana dari penjumlahan suku sejenis tersebut adalah 4ab − 4bc − 5ac (A).

Simak Pembahasan Soal Matematika SMP UN 2018 selengkapnya.

No. 01 - 05	No. 21 - 25
No. 06 - 10	No. 26 - 30
No. 11 - 15	No. 31 - 35
No. 16 - 20	No. 36 - 40

Dapatkan pembahasan soal dalam file pdf  di sini.

Demikian, berbagi pengetahuan bersama Kak Ajaz. Silakan bertanya di kolom komentar apabila ada pembahasan yang kurang jelas. Semoga berkah.