Pembahasan Matematika IPA UN 2019 No. 16 - 20

Pembahasan soal-soal Ujian Nasional (UN) tahun 2019 bidang studi Matematika SMA-IPA nomor 16 sampai dengan nomor 20 tentang:

• turunan fungsi, 
• aplikasi integral (nilai maksimum). 
• aplikasi integral (gradien garis singgung), dan 
• integral substitusi.

Soal No. 16 tentang Turunan Fungsi

Apabila f(x) = 2x² − 10x + 12 maka hasil dari

adalah ….

A.   2x²
B.   4x
C.   4x − 10
D.   4
E.   −10

Pembahasan

Perhatikan rumus di bawah ini!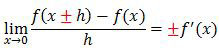

Dengan demikian hasil limit fungsi tersebut adalah turunan dari fungsi f(x).

f(x) = 2x² − 10x + 12
f'(x) = 4x − 10

Jadi, hasil dari limit tersebut adalah 4x − 10 (C).

Perdalam materi ini di Pembahasan Matematika UN: Turunan Fungsi.

Soal No. 17 tentang Aplikasi Turunan (Nilai Maksimum)

Dari selembar karton berbentuk persegi yang berukuran sisi 30 cm akan dibuat kotak tanpa tutup dengan cara menggunting empat persegi di setiap pojok karton seperti pada gambar.

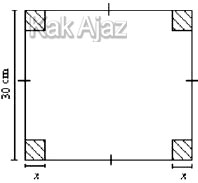
Volume kotak terbesar yang dapat dibuat adalah ….

A.   2.000 cm³
B.   3.000 cm³
C.   4.000 cm³
D.   5.000 cm³
E.   6.000 cm³

Pembahasan

Perhatikan gambar berikut ini!

Berdasarkan gambar, volume kotak tersebut adalah:

V = s² t
   = (30 − 2x)² ∙ x
   = (900 − 120x + 4x²)x
   = 900x − 120x² + 4x³

Agar volume kotak tersebut maksimum maka turunan pertama dari fungsi V harus sama dengan nol.

                          V' = 0
900 − 240x + 12x² = 0
          x − 20x + 75 = 0  [dibagi 12]
       (x − 5)(x − 15) = 0
x = 5 atau x = 15 (tidak mungkin)

Artinya, volume kotak akan maksimum jika x = 5 cm. Sehingga,

V  = (30 − 2x)² ∙ x
    = (30 − 2 ∙ 5)² ∙ 5
    = 400 ∙ 5
    = 2000

Jadi, volume kotak terbesar yang dapat dibuat adalah 2.000 cm³ (A).

Perdalam materi ini di Pembahasan Matematika UN: Aplikasi Turunan.

Soal No. 18 tentang Aplikasi Turunan (Gradien Garis Singgung)

Persamaan garis singgung kurva f(x) = √(2x + 3) yang tegak lurus garis 3x + y − 2 = 0 adalah ….

A.   9x − 3y + 14 = 0
B.   8x − 24y + 39 = 0
C.   3x − y − 6 = 0
D.   3x + y − 12 = 0
E.   x − 3y + 6 = 0

Pembahasan

Gradien garis 3x + y − 2 = 0 adalah:

m₁ = −a/b
      = −3

Sedangkan gradien garis singgung kurva f(x) = √(2x + 3) adalah turunan kurva tersebut.

m₂ = f'(x)
     = 2 ∙ ½ (2x + 3)^−1/2
     = 1/√(2x + 3)

Antara garis singgung kurva dan garis saling tegak lurus sehingga berlaku hubungan:

m₁ ∙ m₂ = −1
        m₂ = −1/m₁
              = −1/(−3)
              = 1/3

Kita sudah mendapatkan gradien garis singgung kurva (m₂). Sekarang kita lanjutkan untuk mencari titik singgung kurva tersebut.

             m₂ = 1/3
1/√(2x + 3) = 1/3
   √(2x + 3) = 3
        2x + 3 = 9
              2x = 6
                x = 3

x = 3 ini adalah absis titik singgung. Mari kita cari ordinat titik singgungnya dengan melakukan substitusi ke kurva f(x)!

f(x) = √(2x + 3)
f(3) = √(2∙3 + 3)
       = 3

Sehingga titik singgung kurva tersebut adalah (3, 3).

Persamaan garis singgung kurva dirumuskan:

      y − y₁ = m₂ (x − x₁)
        y − 3 = 1/3(x − 3)
      3y − 9 = x − 3         [dikalikan 3]
3y − x − 6 = 0
x − 3y + 6 = 0

Jadi, persamaan garis singgung kurva tersebut adalah opsi (E).

Perdalam materi ini di Pembahasan Matematika UN: Aplikasi Turunan.

Soal No. 19 tentang Aplikasi Turunan (Gradien Garis singgung)

Persamaan garis yang melalui A(1, 1) dan tegak lurus dengan garis singgung kurva f(x) = x³ − 3x² + 3 di titik tersebut adalah ….

A.   y + 3x − 4 = 0
B.   y + 3x − 2 = 0
C.   3y − x + 2 = 0
D.   3y − x − 2 = 0
E.   3y − x − 4 = 0

Pembahasan

Gradien garis singgung kurva f(x) = x³ − 3x² + 3 adalah:

m₁ = f'(x)
     = 3x² − 6x

Substitusi absis x = 1 diperoleh:

m₁ = 3 ∙ 1² − 6∙1
     = −3

Karena garis dan garis singgung kurva saling tegak lurus maka:

m₁ ∙ m₂ = −1
        m₂ = −1/m₁
              = −1/(−3)
              = 1/3

Dengan demikian, persamaan garis tersebut adalah:

       y − y₁ = m₂ (x − x₁)
        y − 1 = 1/3(x − 1)
      3y − 3 = x − 1        [dikalikan 3]
3y − x − 2 = 0

Jadi, persamaan garis tersebut adalah opsi (D).

Perdalam materi ini di Pembahasan Matematika UN: Aplikasi Turunan.

Soal No. 20 tentang Integral Substitusi

Hasil dari ∫(8x − 6)(2x² − 3x − 2) dx = ….

A.   2(2x² − 3x − 2)⁴ + C
B.   ½ (2x² − 3x − 2)⁴ + C
C.   ¼ (2x² − 3x − 2)⁴ + C
D.   (2x² − 3x − 2)² + C
E.   ⅔ (2x² − 3x − 2)⁴ + C

Pembahasan

Integral di atas termasuk integral substitusi. Cirinya, terdiri dari dua fungsi dengan derajat (pangkat tertinggi) berselisih satu.

Adapun cara penyelesaiannya sebagai berikut:

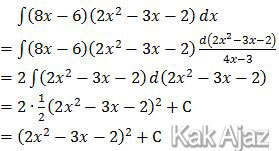
Jadi, hasil dari integral tersebut adalah (D).

Perdalam materi ini di Pembahasan Matematika UN: Integral Aljabar.

Simak Pembahasan Soal Matematika IPA UN 2019 selengkapnya.

No. 01 - 05	No. 21 - 25
No. 06 - 10	No. 26 - 30
No. 11 - 15	No. 31 - 36
No. 16 - 20	No. 37 - 40

Dapatkan pembahasan soal dalam file pdf  di sini.

Demikian, berbagi pengetahuan bersama Kak Ajaz. Silakan bertanya di kolom komentar apabila ada pembahasan yang kurang jelas. Semoga berkah.