Pembahasan Matematika IPA UN 2019 No. 1 - 5

Pembahasan soal-soal Ujian Nasional (UN) tahun 2019 bidang studi Matematika SMA-IPA nomor 1 sampai dengan nomor 5 tentang:

• sistem persamaan linear, 
• sistem pertidaksamaan linear (model matematika), 
• sistem pertidaksamaan linear (daerah penyelesaian), 
• program linear, dan 
• fungsi kuadrat.

Soal No. 1 tentang Sistem Persamaan Linear

Harga tiket masuk sebuah pertunjukan adalah Rp100.000,00 untuk dewasa dan Rp40.000,00 untuk anak-anak. Pada suatu hari, sebanyak 300 orang datang menyaksikan pertunjukan dan diperoleh Rp19.200.000,00 dari hasil penjualan tiket. Jumlah orang dewasa dan anak-anak yang datang ke pertunjukan pada hari itu adalah ….

A.   120 orang dewasa dan 180 anak-anak
B.   180 orang dewasa dan 120 anak-anak
C.   230 orang dewasa dan 70 anak-anak
D.   160 orang dewasa dan 140 anak-anak
E.   140 orang dewasa dan 160 anak-anak

Pembahasan

Model matematika untuk soal di atas adalah:

x + y = 300                                     … (1)
100.000x + 40.000y = 19.200.000 … (2)

Dengan mengalikan 4 pada persamaan (1) dan membagi 10.000 pada persamaan (2) diperoleh:

  4x + 4y = 1200
10x + 4y = 1920
⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯  − (bawah dikurangi atas)
          6x = 720
            x = 120

Substitusi x = 120 persamaan (1) diperoleh:

120 + y = 300
          y = 180

Jadi, jumlah orang dewasa dan anak-anak yang datang ke pertunjukan pada hari itu adalah 120 orang dewasa dan 180 anak-anak (A).

Perdalam materi ini di Pembahasan Matematika IPA UN: Sistem Persamaan Linear.

Soal No. 2 tentang Sistem Pertidaksamaan Linear

Perhatikan gambar berikut!

Daerah yang diarsir pada gambar di atas merupakan daerah penyelesaian dari sistem pertidaksamaan ….

A.   x + 2y ≥ 8; 2x + 3y ≥12; x ≥ 0; y ≥ 0
B.   2x + y ≥ 8; 3x + 2y ≥ 12; x ≥ 0; y ≥ 0
C.   2x + y ≤ 8; 2x + 3y ≤ 12; x ≥ 0; y ≥ 0
D.   2x + y ≤ 8; 3x + 2y ≤ 12; x ≥ 0; y ≥ 0
E.   x + 2y ≤ 8; 2x + 3y ≤ 12; x ≥ 0; y ≥ 0

Pembahasan

Untuk menentukan persamaan garis dari suatu grafik, gunakan konsep berikut ini!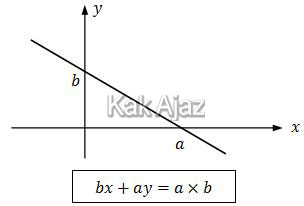

Berdasarkan konsep di atas, persamaan garis pada grafik di bawah ini adalah:

(1)   8x + 4y = 32
(2)   4x + 6y = 24

Jika kedua persamaan di atas disederhanakan maka akan menjadi:

(1)   2x + y = 8
(2)   2x + 3y = 12

Daerah yang diarsir terletak di bawah garis (1) dan di bawah garis (2) sehingga tanda pertidaksamaannya adalah “≤” (kurang dari atau sama dengan).

(1)   2x + y ≤ 8
(2)   2x + 3y ≤ 12

Daerah arsiran tersebut terletak pada kuadran I sehingga semua x dan y bernilai positif.

x ≥ 0; y ≥ 0

Jadi, daerah yang merupakan daerah penyelesaian dari sistem pertidaksamaan di atas adalah opsi (C).

Perdalam materi ini di Sistem Pertidaksamaan Linear [Soal UN dan Pembahasan].

Soal No. 3 tentang Sistem Pertidaksamaan Linear

Perhatikan gambar berikut!

Daerah yang memenuhi sistem pertidaksamaan linear x + y ≤ 4; x + 4y ≥ 8, x ≥ 0, y ≥ 0 adalah ….

A.   I
B.   II
C.   III
D.   IV
E.   V

Pembahasan

Berdasarkan konsep pengerjaan soal nomor 2 maka: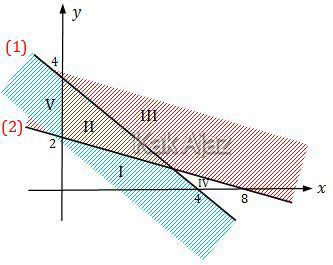

Pertidaksamaan (1) adalah x + y ≤ 4. Karena tanda pertidaksamaannya “≤” maka daerah yang diarsir berada di bawah garis (arsiran biru).

Sedangkan pertidaksamaan (2) adalah x + 4y ≥ 8. Karena tanda pertidaksamaannya “≥” maka daerah yang diarsir berada di atas garis (arsiran merah).

Sementara itu, arsiran warna coklat merupakan irisan pertidaksamaan (1) dan (2) di kuadran I (x ≥ 0, y ≥ 0).

Jadi, daerah yang memenuhi sistem pertidaksamaan linear adalah daerah II (B).

Perdalam materi ini di Sistem Pertidaksamaan Linear [Soal UN dan Pembahasan].

Soal No. 4 tentang Program Linear

Seorang petani akan menanam jagung dan singkong dengan lahan yang dibutuhkan tidak lebih dari 50 petak. Petani tersebut membutuhkan pupuk sebanyak 30 kg per petak untuk memupuk jagung dan 60 kg per petak untuk memupuk singkong. Jumlah pupuk yang tersedia adalah 2.400 kg. Jika keuntungan dari lahan jagung adalah Rp4.000.000,00 per petak dan lahan singkong adalah Rp6.000.000,00 per petak dalam sekali tanam, keuntungan maksimum petani tersebut adalah ….

A.   Rp460.000.000,00
B.   Rp360.000.000,00
C.   Rp325.000.000,00
D.   Rp260.000.000,00
E.   Rp160.000.000,00

Pembahasan

Berikut ini adalah tabel bantuan untuk soal program linear di atas.

Berdasarkan tabel bantuan di atas, model matematikanya adalah:

x + y ≤ 50
x + 2y ≤ 80

Untuk menyelesaikannya, kita ubah ke persamaan kemudian kita eliminasi.

x + y   = 50
x + 2y = 80
⎯⎯⎯⎯⎯⎯⎯  −
        y = 30

Substitusi y = 30 ke persamaan pertama diperoleh:

x + 30 = 50
        x = 20

Sementara itu, fungsi sasaran program linear tersebut adalah:

z = 4.000.000x + 6.000.000y

Sehingga nilainya adalah:

z = 4.000.000×20 + 6.000.000×30
  = 80.000.000+180.000.000
  = 260.000.000

Jadi, keuntungan maksimum petani tersebut adalah Rp260.000.000,00 (D).

Perdalam materi ini di Pembahasan Matematika IPA UN: Program Linear.

Soal No. 5 tentang Fungsi Kuadrat

Perhatikan gambar fungsi f(x) = ax² + bx + c berikut!

Nilai a, b, dan c yang sesuai dengan grafik di atas adalah ….

A.   a > 0, b < 0, dan c < 0
B.   a > 0, b < 0, dan c > 0
C.   a < 0, b > 0, dan c < 0
D.   a < 0, b > 0, dan c > 0
E.   a < 0, b < 0, dan c < 0

Pembahasan

Ketentuan nilai a, b, dan c pada grafik fungsi kuadrat adalah sebagai berikut:

• a > 0 : grafik terbuka ke atas
• a < 0 : grafik terbuka ke bawah
• b > 0 : sumbu simetri sebelah kiri jika a > 0
           sumbu simetri sebelah kanan jika a < 0
• b < 0 : sumbu simetri sebelah kanan jika a > 0
           sumbu simetri sebelah kiri jika a < 0
• c > 0 : memotong sumbu y positif
• c < 0 : memotong sumbu y negatif

Berdasarkan ketentuan di tersebut, grafik di atas adalah:

• terbuka ke bawah : a < 0
• simetri sebelah kiri : b < 0
• memotong sumbu y negatif : c < 0

Jadi, nilai a, b, dan c yang sesuai dengan grafik di atas adalah opsi (E).

Perdalam materi ini di Pembahasan Matematika IPA UN: Fungsi Kuadrat.

Simak Pembahasan Soal Matematika IPA UN 2019 selengkapnya.

No. 01 - 05	No. 21 - 25
No. 06 - 10	No. 26 - 30
No. 11 - 15	No. 31 - 36
No. 16 - 20	No. 37 - 40

Simak juga:
Pembahasan Matematika IPA UN 2019 No. 01 - 05 

Dapatkan pembahasan soal dalam file pdf  di sini.

Demikian, berbagi pengetahuan bersama Kak Ajaz. Silakan bertanya di kolom komentar apabila ada pembahasan yang kurang jelas. Semoga berkah.